🧩Problem 💡: The search algorithm determines the node that contains the key from the binary search tree.

public static nodetype search(nodetype tree, keytype keyin){
    boolean found;
    nodetype p;

    p = tree;

    found = false;

    while (!found){

        if (p.key == keyin){

            found = true;        

        } else if (keyin < p.key){

            p = p.left;    // search the left child

        } else {

            p = p.right;    // search the right child 

        }

    }

    return p;
}

🚀Keywords

Search time is the number of comparisons made to locate a key. The search function determines a tree structure to minimize the average search time.

💡What are the binary search tree characteristics?

During each iteration, comparisons between the search value and the current node key determine whether the target is found or to move left or right. During each comparison, the search will eliminate half of the remaining nodes from the search space, which contributes to a time complexity:

$$O(log(N))$$

N represents the number of nodes in the tree.

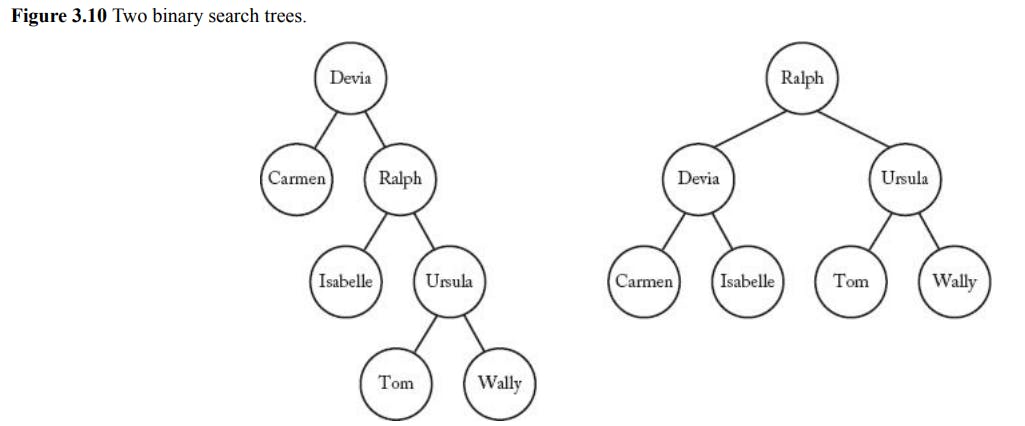
An example is determining the depth of the node "Ursula", a node in the second tree level, and its search time is calculated as:

$$depth(Ursula)+1=2+1=3$$

🌲An optimal binary search tree

🧩Problem: Determine an optimal binary search tree using a set of keys as input.

💡Dynamic programming is a solution for calculating the cumulative probabilities.

def compute_prefix_sums(p):
    n = len(p) - 1
    P = [0] * (n + 1)
    for j in range(1, n + 1):
        P[j] = P[j - 1] + p[j]
    return P

The algorithm has a time complexity of O(n) to iterate through the loop where each computation of P takes O(1).

A prefix sum array is an alternative to calculate the optimal sum of probabilities within a range in O(1) time complexity. If the index is j, the sum is P[j]. Compute a sum for a scope using the equation: "P[j] - P[i - 1]".

Procedure:

1. Initialization:

   Create a prefix sum array P of size n+1, where n is the number of keys.

   Initialize P[0] to 0. This extra element is for easier indexing.

2. Prefix Sum Calculation:

   For i=1 to n:

   P[i]=P[i-1]+pi

3. Using the Prefix Sum Array:

   To compute

$$\sum_{i=1}^{j}p_m$$

The sum is simply P[j].

To compute a sum for a range, say:

$$\sum_{i=1}^{j}p_m$$

The sum is P[j]-P[i-1].

The example allows us to calculate probability sum across any range in a constant time complexity.