🌟Key Terms

Independent

$$x_i, x_j$$

Two variables are independent when a joint distribution could be expressed as a product between two marginal distributions.

$$P(x_i, x_j) = P(x_i)P(x_j)$$

Bayes Theorem

Bayes Theorem or Bayern Munich? 🤔

The probability of an event (x) conditioned on a known event (y) is defined as:

$$P(x | y)=\frac{P(x,y)}{P(y)}$$

Exception

The exceptional condition is when y = 0; the probability is not defined.

Alternative Format

Bayes theorem could be expressed in an alternative format:

$$P(x|y)=\frac{P(y|x)P(x)}{P(y)}$$

Hidden Markov Model

A Hidden Markov Model contains a series of visible and hidden states:

$$V = (v_1,v_2,...,v_T)$$

$$ H=(h_1,h_2,...,h_T)$$

---

💡Common Questions

1. Could a belief network be represented as a directed acyclic graph (DAG)?

2. If there is an edge between two variables in a DAG, does it mean the variables are dependent?

3. Define an EM (Expectation Maximisation) algorithm.

---

📖 Answer 1

When the DAG is presented as:

$$X\rightarrow Y$$

The DAG shows that the Y node is dependent on the X node s.t., the probability distribution is expressed as:

$$P(Y|X)$$

If the following condition holds for every x value:

$$P(Y|X)=P(Y)$$

It is determined that the Y node and the X node are independent even though they are connected.

📖 Answer 2

⏳IN PROGRESS 🔃

📖 Answer 3

💻An EM algorithm computes the maximum likelihood function using an iterative cycle that executes the E and M steps until the parameters converge to the peak value.

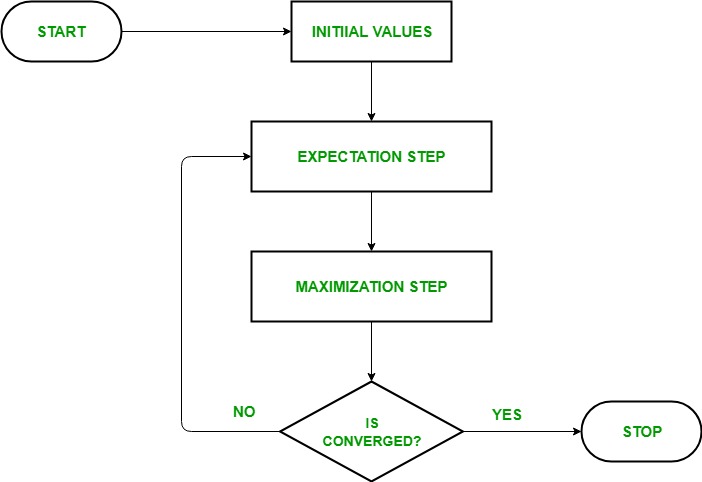
EM-algorithm iterates until the parameters converge to a maximum value:

1. E-step uses the current parameters to calculate a distribution that maximises the likelihood.

2. M-step uses the derived distribution from the E-step to update the parameters, maximising the likelihood.